Tangent-Secant Theorem

The Secant Theorem equations computes the length of a line from a point outside a circle to a tangent point on the circle based on the Tangent-Secant Theorem.

INSTRUCTIONS: Choose units and enter the following:

• (r)  Radius of the circle, where r = 1/2 GE
• (DE) Distance of point D outside the circle

Distance to Tangent  (DC): The calculator returns the distance in meters.  However, this can be automatically converted to compatible units via the pull-down menu.

The Math / Science

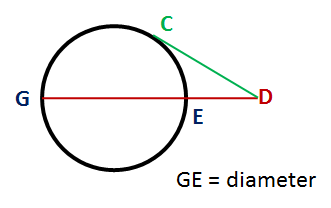
The Tangent-Secant Theorem represents that if a line from a point D outside a circle intersects the circle at exactly one point C (in other words DC is tangent to the circle) and a secant (a line intersecting the circle at two points) from the same external point D meets the circle at points G and E respectively, then DC² = DG × DE as shown in the diagram.

Since the radius of the circle,  r = 1/2 GE, then DG = 2r + DE

So, DC² = (2r +DE) * DE

`DC = sqrt((2r +DE) * DE)`